Problem # 9

The conjecture that the above statement can be answered in the positive is known as the Barendregt-Geuvers-Klop conjecture. It was presented to the originator by Henk Barendregt some time in 1994. Is is stated as (part of) Conjecture 8.1.2 in [Geuvers, 1993].

A partial solution, conﬁrming that the conjecture is true for a certain class of non-dependent systems, appeared in [Sørensen, 1997, Barthe et al., 2001].

It is natural to wonder how the result can be extended to larger classes of pure type systems. An obvious line of attack is to study translations that eliminate dependency, and to establish preservation of the necessary normalization properties (see Deﬁnition 6.5.23 in [Geuvers, 1993] for a translation eliminating dependency in the cube).

Another idea, which will probably only lead to marginal improvements, is to replace the CPS-translation of [Sørensen, 1997, Barthe et al., 2001] by a simpler thunkiﬁcation translation or another translation with similar properties (see [Gørtz et al., 2003]).

A related conjecture is the so-called K-conjecture [Barthe, 1995], which is shown to follow from the Barendregt-Geuvers-Klop conjecture within the class of functional pure type systems [Barthe, 1998].

References for # 9

[Barthe, 1995] Barthe, G. (1995). Extensions of Pure Type Systems. In Dezani-Ciancaglini, M. and Plotkin, G., editors, Typed Lambda Calculi and Applications, volume 902 of Lecture Notes in Computer Science, pages 16–31. Springer-Verlag.

[Barthe, 1998] Barthe, G. (1998). The semi-full closure of Pure Type Systems. In Brim, L., Gruska, J., and Zlatuska, J., editors, Proceedings of MFCS’98, volume 1450 of Lecture Notes in Computer Science, pages 316–325. Springer-Verlag.

[Barthe et al., 2001] Barthe, G., Hatcliff, J., and Sørensen, M. H. (2001). Weak normalization implies strong normalization in a class of non-dependent pure type systems. Theoretical Computer Science, 269(1–2):317–361.

[Geuvers, 1993] Geuvers, H. (1993). Logics and Type Systems. PhD thesis, Nijmegen University.

[Gørtz et al., 2003] Gørtz, I. L., Reuss, S., and Sørensen, M. H. (2003). Strong normalization from weak normalization by translation into the lambda-I-calculus. Higher Order Symbol. Comput., 16(3):253–285.

[Ketema et al., 2005] Ketema, J., Klop, J. W., and van Oostrom, V. (2005). Vicious circles in orthogonal term rewriting systems. Electronic Notes in Computer Science, 124(2):65–77.

[Sørensen, 1997] Sørensen, M. (1997). Normalization in 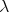$λ$ -Calculus and Type Theory. PhD thesis, Department of Computer Science, University of Copenhagen. Available as DIKU Rapport 97/27.