Date: 2000
Statement. How many fixed points can a combinator have?
Problem Origin. First posed in [Intrigila and Biasone, 2000].
Submitted by Benedetto Intrigila
Date: 2000
Statement. How many fixed points can a combinator have?
Problem Origin. First posed in [Intrigila and Biasone, 2000].
The question is how many fixed points can a combinator (i.e. a closed term)
have in the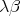 
-calculus. In [Intrigila and Biasone, 2000] it is proved that, if
a combinator has a fixed point in normal form then, it has either an infinite
number of fixed points or exactly one fixed point.
[Intrigila and Biasone, 2000] Intrigila, B. and Biasone, E. (2000). On the number of fixed points of a combinator in lambda calculus. Mathematical Structures in Computer Science, 10(5):595–615.