Date: 2013
Statement. On the equational meaning of deeds
Problem Origin. The problem has been posed first by Corrado Böhm . It is added to the list to celebrate his 90th birthday.
Submitted by Corrado Böhm
Date: 2013
Statement. On the equational meaning of deeds
Problem Origin. The problem has been posed first by Corrado Böhm . It is
added to the list to celebrate his 90th birthday.
A deed is a closed normal form with only one initial abstraction, namely a deed
has shape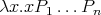 
where 
.
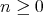It is easy to verify that each equation of the shape
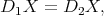
where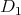 
, 
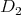are deeds, can be solved, for instance by choosing a fixed point of
the combinator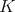 
as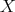 
.
It it possible to define a one-one mapping between arbitrary normal forms and
deeds, as follows. Given a normal form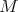 
with 
initial abstractions, the
deed corresponding to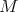 
is:
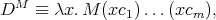
are the Church numerals or any distinct closed beta-eta normal
forms. Note that the mapping is injective by Böhm’s theorem.
The question is as follows: What can we understand about the solution of the
equation 
, where 
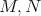are arbitrary normal forms, by looking at
the equation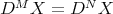 
?