[Next] [Previous] [Up]
Problem # 7
Submitted by Richard Statman
Date: 1993
Statement. Word problem for combinators of orders less than 3.
[PRINT this PROBLEM]
The word problem for a set of combinators  is to determine if two applicative
combinations of members of
is to determine if two applicative
combinations of members of  are
are 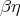 -equal. A proper combinator
-equal. A proper combinator 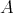 , with
reduction rule
, with
reduction rule 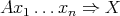 , where
, where 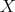 is an applicative combination of
is an applicative combination of
 is said to have order
is said to have order 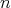 . We ask if the word problem for all proper
combinators of orders less than 3 is decidable. The problem was originally
proposed in [Statman, 1989].
. We ask if the word problem for all proper
combinators of orders less than 3 is decidable. The problem was originally
proposed in [Statman, 1989].
Comments by Richard Statman: It is easy to see that the word problem for
combinators of order 1 is decidable. More can be shown [Statman, 1988a].
In [Statman, 1989] it is shown that the word problem for Smullyan’s Lark
combinator is solvable even though fixed points always exist. In [Statman, 2000]
we prove that the word problem for all co-compositors and finitely many
instances of (finitely many) compositors is solvable. We have been led to the
conjecture: The word problem for all proper combinators of order less than 3
(taken together in one system) is decidable. Some combinator of order 3
or more is necessary for a basis of proper combinators [Statman, 1986]
but slightly beyond order 2 [Statman, 1988b] leads to undecidabilty.
Added “in proof”: This problem also occurs in the RTA LOOP as problem
number 96.
References for # 7
[Statman, 1986] Statman, R. (1986). On translating lambda terms
into combinators. In Logic in Computer Science, pages 378–382. IEEE
Computer Society Press.
[Statman, 1988a] Statman, R. (1988a). Combinators hereditarily of
order one. Technical Report 88-32, Department of Mathematics, Carnegie
Mellon University.
[Statman, 1988b] Statman, R. (1988b). Combinators hereditarily of
order two. Technical Report 88-33, Department of Mathematics, Carnegie
Mellon University.
[Statman, 1989] Statman, R. (1989). The word problem for Smullyan’s
Lark combinator is decidable. Journal of Symbolic Computation,
7(2):103–112.
[Statman, 2000] Statman, R. (2000). On the word problem for
combinators. In Rewriting Techniques and Applications, volume 1833 of
Lecture Notes in Computer Science, pages 203–213. Springer-Verlag.
[Next] [Previous] [Up]
Last modified: July 21, 2014
 is to determine if two applicative
combinations of members of
is to determine if two applicative
combinations of members of  are
are 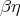 -equal. A proper combinator
-equal. A proper combinator 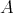 , with
reduction rule
, with
reduction rule 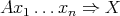 , where
, where 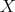 is an applicative combination of
is an applicative combination of
 is said to have order
is said to have order 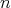 . We ask if the word problem for all proper
combinators of orders less than 3 is decidable. The problem was originally
proposed in [Statman, 1989].
. We ask if the word problem for all proper
combinators of orders less than 3 is decidable. The problem was originally
proposed in [Statman, 1989].