[Next] [Previous] [Up]
Problem # 6
Submitted by Richard Statman
Date: 1993
Statement. Basis Decision Problem.
[PRINT this PROBLEM]
The basis decision problem, originally stated in [Statman, 1993], is to
decide whether a given finite set of proper combinators is combinatorially
complete. (A proper combinator [Barendregt, 1984, p. 184] is one of the form
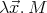 , where
, where 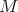 contains no lambda, and
contains no lambda, and 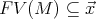 .) It follows from
Theorem 4 in [Statman, 1986] that the problem is undecidable for finite sets
of normal (possibly improper) combinators. A good solution would be
an abstraction algorithm, parameterized by a given set of combinators,
which returned an error message on non-bases. Broda and Damas have
proved that in the linear case the problem is decidable [Broda and Damas,
1997].
.) It follows from
Theorem 4 in [Statman, 1986] that the problem is undecidable for finite sets
of normal (possibly improper) combinators. A good solution would be
an abstraction algorithm, parameterized by a given set of combinators,
which returned an error message on non-bases. Broda and Damas have
proved that in the linear case the problem is decidable [Broda and Damas,
1997].
References for # 6
[Barendregt, 1984] Barendregt, H. (1984). The Lambda Calculus. Its
Syntax and Semantics. North-Holland, second edition.
[Broda and Damas, 1997] Broda, S. and Damas, L. (1997). On
combinatory complete sets of proper combinators. Journal of Functional
Programming, 7(6):593–612.
[Statman, 1986] Statman, R. (1986). On translating lambda terms
into combinators. In Logic in Computer Science, pages 378–382. IEEE
Computer Society Press.
[Statman, 1993] Statman, R. (1993). Some examples of non-existent
combinators. Theoretical Computer Science, 121:441–448.
[Next] [Previous] [Up]
Last modified: July 21, 2014
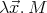 , where
, where 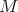 contains no lambda, and
contains no lambda, and 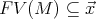 .) It follows from
Theorem 4 in [Statman, 1986] that the problem is undecidable for finite sets
of normal (possibly improper) combinators. A good solution would be
an abstraction algorithm, parameterized by a given set of combinators,
which returned an error message on non-bases. Broda and Damas have
proved that in the linear case the problem is decidable [Broda and Damas,
1997].
.) It follows from
Theorem 4 in [Statman, 1986] that the problem is undecidable for finite sets
of normal (possibly improper) combinators. A good solution would be
an abstraction algorithm, parameterized by a given set of combinators,
which returned an error message on non-bases. Broda and Damas have
proved that in the linear case the problem is decidable [Broda and Damas,
1997].