Date: 1993
Statement. Does the typability hierarchy of
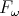collapse on 
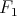? Submitted by Paweł Urzyczyn
Date: 1993
Statement. Does the typability hierarchy of 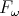collapse on ?
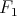The type assignment system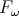 
can be split into an infinite hierarchy of
subsystems 
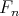(see [Girard, 1986]), where 
is the usual polymorphic
lambda-calculus (system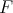 
), and 
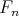admits constructors of order 
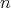. (A type
is a constructor of order zero, a constructor of order one is a function acting on
types, and a constructor of order 
has arguments of order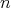 
.) It is
conjectured [Urzyczyn, 1997] that every pure lambda-term typable in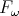 
is
typable already in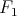 
.
Remark: An incorrect proof of the conjecture appeared in [Malecki, 1997].
[Girard, 1986] Girard, J.-Y. (1986). The system F of variable types, fifteen years later. Theoretical Computer Science, 45:159–192.
[Malecki, 1997] Malecki, S. (1997). Proofs in syste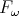m 
can be done in
system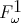 
. In van Dalen, D. and Bezem, M., editors, Computer Science
Logic, volume 1258 of Lecture Notes in Computer Science, pages 297–315.
Springer-Verlag.
[Urzyczyn, 1997] Urzyczyn, P. (1997). Type reconstruction in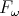 
.
Mathematical Structures in Computer Science, 7(4):329–358.