Date: 1993
Statement. Which equations on intersection types preserve normalization?
Problem Origin. Included in the list of open problems from the “Gentzen” meeting in 1993. Author unknown.
Submitted by Paweł Urzyczyn
Date: 1993
Statement. Which equations on intersection types preserve normalization?
Problem Origin. Included in the list of open problems from the “Gentzen”
meeting in 1993. Author unknown.
Let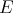 
be a finite set of equations between intersection types, and let 
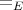be
the congruence generated by 
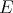. Extend intersection type assignment by the
rule:
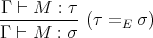
Under what condition such a type assignment system has the (strong) normalization
property? As an example consider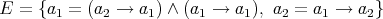 
.
This system is not “positive” or “monotone” (cf. Problem 1) yet it is believed to
be strongly normalizing. Note: As shown in [Mendler, 1991], positivity is
a necessary and sufficient condition for strong normalization of a system defined
by equations between simple types (without intersections).
[Mendler, 1991] Mendler, N. (1991). Inductive types and type constraints in the second-order lambda calculus. Annals of Pure and Applied Logic, 51(1-2):159–172.