Date: 1993–2006
Statement. Inhabitation for intersection type systems

Problem Origin. Different variants of the problem were stated by Henk Barendregt, Mariangiola Dezani-Ciancaglini, Paula Severi, Paweł Urzyczyn, and others.
Submitted by Mariangiola Dezani-Ciancaglini
Date: 1993–2006
Statement. Inhabitation for intersection type systems 
Problem Origin. Different variants of the problem were stated by Henk
Barendregt, Mariangiola Dezani-Ciancaglini, Paula Severi, Paweł Urzyczyn,
and others.
The inhabitation problem is to determine whether there exists a closed term of a given type. [Urzyczyn, 1999] shows the undecidability of inhabitation for the intersection type system of [Barendregt et al., 1983]. Decidable restrictions are discussed in [Kurata and Takahashi, 1995].
Many different intersection type systems have been introduced, mainly for
describing 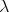 -models: for a list see [Alessi et al., 2006] and the references there.
A natural question is decidability of inhabitation for these systems. Using the
notation of [Alessi et al., 2006], undecidability of the inhabitation for the system
of [Barendregt et al., 1983] implies undecidability of the inhabitation
for the systems
-models: for a list see [Alessi et al., 2006] and the references there.
A natural question is decidability of inhabitation for these systems. Using the
notation of [Alessi et al., 2006], undecidability of the inhabitation for the system
of [Barendregt et al., 1983] implies undecidability of the inhabitation
for the systems 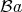 ,
, 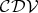 ,
, 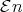 . It is easy to show that all types are
inhabited in
. It is easy to show that all types are
inhabited in 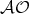 and
and 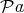 systems, since all terms inhabit the top type
and all closed terms inhabit the bottom type [Honsell and Ronchi Della
Rocca, 1992]. A similar argument shows decidability for
systems, since all terms inhabit the top type
and all closed terms inhabit the bottom type [Honsell and Ronchi Della
Rocca, 1992]. A similar argument shows decidability for 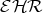 system.
The question remains open for the systems
system.
The question remains open for the systems 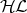 ,
, 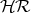 ,
, 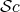 ,
, 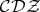 ,
,
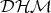 .
.
A related issue is the inhabitation problem for intersection types of rank at most 3, according to the classification of [Leivant, 1983]. The undecidability proof in [Urzyczyn, 1999] works for rank 4, the problem for rank 2 is decidable, but Exptime-hard [Kuśmierek, 2007].
Yet another open question is the inhabitation problems for systems with recursive intersection types, cf. Problem 11.
Partial solution: The inhabitation problem turned out to be undecidable for types of rank 3 and Expspace-complete for rank 2 [Urzyczyn, 2009].
[Alessi et al., 2006] Alessi, F., Barbanera, F., and Dezani-Ciancaglini, M. (2006). Intersection types and lambda models. Theoretical Computer Science, 355(2):108–126.
[Barendregt et al., 1983] Barendregt, H., Coppo, M., and Dezani-Ciancaglini, M. (1983). A filter lambda model and the completeness of type assignment. Journal of Symbolic Logic, 48(4):931–940.
[Honsell and Ronchi Della Rocca, 1992] Honsell, F. and Ronchi Della Rocca, S. (1992). An approximation theorem for topological lambda models and the topological incompleteness of lambda calculus. Journal of Computer and System Sciences, 45(1):49–75.
[Kurata and Takahashi, 1995] Kurata, T. and Takahashi, M. (1995). Decidable properties of intersection type systems. In Dezani-Ciancaglini, M. and Plotkin, G., editors, Typed Lambda Calculi and Applications, volume 902 of Lecture Notes in Computer Science, pages 297–311. Springer-Verlag.
[Kuśmierek, 2007] Kuśmierek, D. (2007). The inhabitation problem for rank two intersection types. In Ronchi Della Rocca, S., editor, Typed Lambda Calculi and Applications, volume 4583 of Lecture Notes in Computer Science, pages 240–254. Springer-Verlag.
[Leivant, 1983] Leivant, D. (1983). Polymorphic type inference. In Symposium on Principles of Programming Languages, pages 88–98. ACM Press.
[Urzyczyn, 1999] Urzyczyn, P. (1999). The emptiness problem for intersection types. Journal of Symbolic Logic, 64(3):1195–1215. (Preliminary version in Proc. LICS 94).
[Urzyczyn, 2009] Urzyczyn, P. (2009). Inhabitation of low-rank intersection types. In Curien, P.-L., editor, Typed Lambda Calculi and Applications, volume 5608 of Lecture Notes in Computer Science, pages 356–370. Springer-Verlag.