Date: 1995
Statement. Is the equational theory of typed
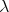 -calculus with finite sums the
maximum consistent typically-ambiguous congruence?
-calculus with finite sums the
maximum consistent typically-ambiguous congruence? 
Problem Origin. The problem was posed by Alex Simpson and probably others.
Submitted by Alex Simpson
Date: 1995
Statement. Is the equational theory of typed 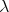 -calculus with finite sums the
maximum consistent typically-ambiguous congruence?
-calculus with finite sums the
maximum consistent typically-ambiguous congruence? 
Problem Origin. The problem was posed by Alex Simpson and probably
others.
Extend the simply-typed 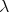 -calculus with syntax for finite product and sum
types. This has a standard notion of
-calculus with syntax for finite product and sum
types. This has a standard notion of 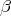 -equality,
-equality, 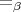 . By
. By 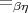 we mean the
equational theory induced semantically by interpretations in bicartesian closed
categories (cartesian closed categories with finite coproducts ). It is not hard to
axiomatize this equality. Following [Statman, 1983], a typed congruence relation
we mean the
equational theory induced semantically by interpretations in bicartesian closed
categories (cartesian closed categories with finite coproducts ). It is not hard to
axiomatize this equality. Following [Statman, 1983], a typed congruence relation
 , is said to be typically ambiguous if it is preserved under type substitutions;
that is:
, is said to be typically ambiguous if it is preserved under type substitutions;
that is: 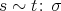 implies
implies 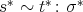 , where the
, where the 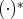 transformation
performs a substitution of types for atomic types. The main question
is:
transformation
performs a substitution of types for atomic types. The main question
is:
Is 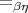 maximum amongst consistent typically-ambiguous
congruence relations containing
maximum amongst consistent typically-ambiguous
congruence relations containing 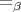 ?
?
A (possibly) weaker version of the question is simply: is it the case that the only
typically-ambiguous congruence relation properly extending 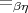 is the
inconsistent relation? There are various semantic equivalents to and consequences
of a positive answer to this latter question. An equivalent statement is: given any
bicartesian-closed category
is the
inconsistent relation? There are various semantic equivalents to and consequences
of a positive answer to this latter question. An equivalent statement is: given any
bicartesian-closed category  that is not a preorder, the equational theory
induced by all interpretations in
that is not a preorder, the equational theory
induced by all interpretations in  is exactly
is exactly 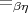 ; see [Simpson, 1995] for a
similar equivalence for the calculus without coproducts. In fact, it is enough to
consider only the category of finite sets; that is, another equivalent is: the
equational theory induced by interpretations in the category of finite sets is
exactly
; see [Simpson, 1995] for a
similar equivalence for the calculus without coproducts. In fact, it is enough to
consider only the category of finite sets; that is, another equivalent is: the
equational theory induced by interpretations in the category of finite sets is
exactly 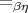 . (To show that this implies that
. (To show that this implies that 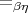 is maximal amongst
consistent typically-ambiguous congruences, one encodes the category of finite sets
within the type theory using finite coproducts of the unit type.) The last
equivalent above is simply the finite model property for
is maximal amongst
consistent typically-ambiguous congruences, one encodes the category of finite sets
within the type theory using finite coproducts of the unit type.) The last
equivalent above is simply the finite model property for 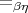 , a standard
consequence of which is decidability. A related result, the decidability
of
, a standard
consequence of which is decidability. A related result, the decidability
of 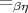 in the case of non-empty coproducts is known from [Ghani,
1995] and [Altenkirch et al., 2001]. Again for non-empty sums only, the
completeness of
in the case of non-empty coproducts is known from [Ghani,
1995] and [Altenkirch et al., 2001]. Again for non-empty sums only, the
completeness of 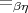 with respect to interpretations in the category of sets
was shown by [Dougherty and Subrahmanyam, 2000]; their argument
makes essential use of infinite sets. A fragment of completeness relative
to finite sets has been shown by [Altenkirch and Uustalu, 2004], who
established completeness and decidability results for the extension of
typed
with respect to interpretations in the category of sets
was shown by [Dougherty and Subrahmanyam, 2000]; their argument
makes essential use of infinite sets. A fragment of completeness relative
to finite sets has been shown by [Altenkirch and Uustalu, 2004], who
established completeness and decidability results for the extension of
typed 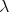 -calculus with a base type of booleans, but without other atomic
types.
-calculus with a base type of booleans, but without other atomic
types.
[Altenkirch et al., 2001] Altenkirch, T., Dybjer, P., Hofmann, M., and Scott, P. (2001). Normalization by evaluation for typed lambda calculus with coproducts. In Logic in Computer Science, pages 303–310. IEEE Computer Society Press.
[Altenkirch and Uustalu, 2004] Altenkirch, T. and Uustalu, T. (2004).
Normalization by evaluation for 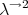 . In Functional and Logic
Programming, volume 2998 of Lecture Notes in Computer Science, pages
260–275.
. In Functional and Logic
Programming, volume 2998 of Lecture Notes in Computer Science, pages
260–275.
[Dezani-Ciancaglini and Plotkin, 1995] Dezani-Ciancaglini, M. and Plotkin, G., editors (1995). Typed Lambda Calculi and Applications, volume 902 of Lecture Notes in Computer Science. Springer-Verlag.
[Dougherty and Subrahmanyam, 2000] Dougherty, D. and Subrahmanyam, R. (2000). Equality between functionals in the presence of coproducts. Information and Computation, 157:52–83.
[Ghani, 1995] Ghani, N. (1995). Beta-eta equality for coproducts. In [Dezani-Ciancaglini and Plotkin, 1995], pages 171–185.
[Simpson, 1995] Simpson, A. (1995). Categorical completeness results
for simply-typed 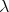 -calculus. In [Dezani-Ciancaglini and Plotkin, 1995],
pages 414–427.
-calculus. In [Dezani-Ciancaglini and Plotkin, 1995],
pages 414–427.
[Statman, 1983] Statman, R. (1983). 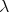 -definable functionals and
-definable functionals and 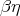 conversion. Archiv für Mathematische Logik und Grundlagenforschung,
23:21–26.
conversion. Archiv für Mathematische Logik und Grundlagenforschung,
23:21–26.