Date: 1996
Statement. Is the subtype entailment problem decidable?

Problem Origin. First stated in [Pottier, 1996] and [Trifonov and Smith, 1996]. The present formulation is from [Henglein and Rehof, 1998].
Submitted by Jakob Rehof
Date: 1996
Statement. Is the subtype entailment problem decidable? 
Problem Origin. First stated in [Pottier, 1996] and [Trifonov and Smith,
1996]. The present formulation is from [Henglein and Rehof, 1998].
We ask if the entailment problem with simple subtyping constraints over
non-structurally ordered trees is decidable. Non-structurally ordered trees have a
least element,  , and a greatest element,
, and a greatest element, 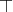 , which can be compared to any
tree regardless of its tree domain (shape). Simple type expressions,
, which can be compared to any
tree regardless of its tree domain (shape). Simple type expressions,  , are finite
terms built from
, are finite
terms built from  ,
, 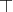 and a binary constructor. Such expressions can be
interpreted as denoting trees, and formal inequality constraints of the form
and a binary constructor. Such expressions can be
interpreted as denoting trees, and formal inequality constraints of the form
 can consequently be valuated in the non-structural order on trees. For a
finite set of constraints
can consequently be valuated in the non-structural order on trees. For a
finite set of constraints  of constraints and terms
of constraints and terms  and
and 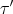 ,
we consider the entailment
,
we consider the entailment 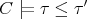 , or, equivalently, validity of the
first-order Horn implication
, or, equivalently, validity of the
first-order Horn implication  , where
, where 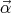 are the
variables occurring in
are the
variables occurring in  ,
,  and
and 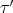 .
.
The problem first appears in slightly different forms in the papers [Pottier, 1996] and [Trifonov and Smith, 1996] for the purpose of simplifying subtyping constraints. It was studied in the form presented here in [Henglein and Rehof, 1998] (following the formulation in [Henglein and Rehof, 1997] for simple types), where it was shown to be to be PSPACE-hard. The full first-order theory of subtyping constraints has been shown to be undecidable [Su et al., 2002], but the question of decidability of entailment remains open [Rehof, 1998]. Further references can be found in [Rehof, 1998] and [Niehren and Priesnitz, 2003].
[Henglein and Rehof, 1997] Henglein, F. and Rehof, J. (1997). The complexity of subtype entailment for simple types. In Logic in Computer Science, pages 352–361. IEEE Computer Society Press.
[Henglein and Rehof, 1998] Henglein, F. and Rehof, J. (1998). Constraint automata and the complexity of recursive subtype entailment. In International Colloquium on Automata, Languages, and Programming, volume 1443 of Lecture Notes in Computer Science, pages 616–627. Springer-Verlag.
[Niehren and Priesnitz, 2003] Niehren, J. and Priesnitz, T. (2003). Non-structural subtype entailment in automata theory. Information and Computation, 186(2):319–354.
[Pottier, 1996] Pottier, F. (1996). Simplifying subtyping constraints. In International Conference on Functional Programming, pages 122–133. ACM Press.
[Rehof, 1998] Rehof, J. (1998). The Complexity of Simple Subtyping Systems. PhD thesis, Department of Computer Science, University of Copenhagen.
[Su et al., 2002] Su, Z., Aiken, A., Niehren, J., Priesnitz, T., and Treinen, R. (2002). The first-order theory of subtyping constraints. In Symposium on Principles of Programming Languages, pages 203–216. ACM Press.
[Trifonov and Smith, 1996] Trifonov, V. and Smith, S. (1996). Subtyping constrained types. In Static Analysis Symposium, volume 1145 of Lecture Notes in Computer Science, pages 349–365. Springer-Verlag.