Date: 1999
Statement. Can recursive types be defined in system
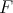 ?
? Submitted by Paweł Urzyczyn
Date: 1999
Statement. Can recursive types be defined in system 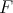 ?
?
It was shown by Geuvers and Spławski that inductive types in the style
of [Mendler, 1991] are definable in the polymorphic 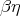 -lambda-calculus. It is
however an open question whether recursive types as in [Mendler, 1987] are also
definable. In [Spławski and Urzyczyn, 1999] it is shown that system
-lambda-calculus. It is
however an open question whether recursive types as in [Mendler, 1987] are also
definable. In [Spławski and Urzyczyn, 1999] it is shown that system 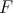 with
with
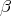 -conversion only is not sufficient for this purpose. See also the paper [Regnier
and Urzyczyn, 2001] and Problem 21.
-conversion only is not sufficient for this purpose. See also the paper [Regnier
and Urzyczyn, 2001] and Problem 21.
[Mendler, 1987] Mendler, N. (1987). Recursive types and type constraints in second-order lambda calculus. In Logic in Computer Science, pages 30–36. IEEE Computer Society Press.
[Mendler, 1991] Mendler, N. (1991). Inductive types and type constraints in the second-order lambda calculus. Annals of Pure and Applied Logic, 51(1-2):159–172.
[Regnier and Urzyczyn, 2001] Regnier, L. and Urzyczyn, P. (2001). Retractions of types with many atoms. Technical Report 29, IML Marseille. http://arxiv.org/abs/cs/0212005.
[Spławski and Urzyczyn, 1999] Spławski, Z. and Urzyczyn, P. (1999). Type fixpoints: Iteration vs. recursion. In International Conference on Functional Programming, pages 102–113. ACM Press.