Date: 2001–2005
Statement. Find trees representing contextual equivalences

Problem Origin. Stated by Mariangiola Dezani, Paula Severi and Fer-Jan de Vries.
Submitted by Mariangiola Dezani-Ciancaglini
Date: 2001–2005
Statement. Find trees representing contextual equivalences 
Problem Origin. Stated by Mariangiola Dezani, Paula Severi and Fer-Jan de
Vries.
If 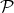 is a set of
is a set of 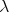 -terms, the contextual equivalence
-terms, the contextual equivalence 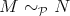 is defined
by:
is defined
by:
![′
C[M ] - → M ∈ 𝒫](opltlca250x.png) if and only if
if and only if ![′
C[N ] - → N ∈ 𝒫](opltlca251x.png) for all contexts
for all contexts ![C[ ]](opltlca252x.png) ,
,
where  denotes
denotes 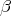 -reduction.
-reduction.
[Wadsworth, 1976] shows that 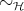 , where
, where 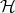 is the set of head normal
forms, coincides with Böhm trees equality (up to infinite
is the set of head normal
forms, coincides with Böhm trees equality (up to infinite 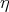 ’s). [Hyland, 1976]
shows that
’s). [Hyland, 1976]
shows that 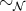 , where
, where 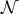 is the set of normal forms, coincides with Böhm
trees equality (up to finite
is the set of normal forms, coincides with Böhm
trees equality (up to finite 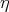 ’s).
’s).
The question is to find tree representations of 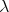 -terms whose equalities
coincide with the following contextual equivalences:
-terms whose equalities
coincide with the following contextual equivalences:
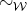 where
where 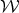 is the set of weak head normal forms,
is the set of weak head normal forms,
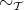 , where
, where 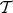 is the set of top normal forms,
is the set of top normal forms,
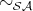 , where
, where 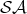 is the set of strongly active terms,
is the set of strongly active terms,
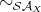 , where
, where 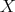 is a set of
is a set of 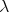 -terms and
-terms and 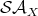 is the set of strongly
active terms depending on
is the set of strongly
active terms depending on 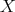 ,
,
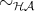 , where
, where 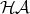 is the set of head active terms.
is the set of head active terms.
The set 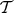 is defined in [Berarducci, 1996], and the sets
is defined in [Berarducci, 1996], and the sets 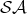 ,
, 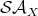 ,
, 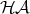 are defined in [Severi and de Vries, 2005, Kennaway et al., 2005].
are defined in [Severi and de Vries, 2005, Kennaway et al., 2005].
[Berarducci, 1996] Berarducci, A. (1996). Infinite 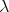 -calculus and
non-sensible models. In Ursini, A. and Aglianò, P., editors, Logic and
Algebra (Pontignano, 1994), pages 339–377. Dekker.
-calculus and
non-sensible models. In Ursini, A. and Aglianò, P., editors, Logic and
Algebra (Pontignano, 1994), pages 339–377. Dekker.
[Hyland, 1976] Hyland, M. (1976). A syntactic characterization of the equality in some models for the lambda calculus. J. London Math. Soc. (2), 12(3):361–370.
[Kennaway et al., 2005] Kennaway, J., Severi, P., Sleep, M., and de Vries, F. J. (2005). Infinite rewriting: from syntax to semantics. In Processes, Terms and Cycles: Steps on the Road to Infinity: Essays Dedicated to Jan Willem Klop on the Occasion of His 60th Birthday, volume 3838 of Lecture Notes in Computer Science, pages 148–172. Springer-Verlag.
[Severi and de Vries, 2005] Severi, P. and de Vries, F. J. (2005). Order structures for Böhm-like models. In Computer Science Logic, volume 3634 of Lecture Notes in Computer Science, pages 103–116. Springer-Verlag.
[Wadsworth, 1976] Wadsworth, C. P. (1976). The relation between
computational and denotational properties for Scott’s 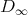 -models of the
lambda-calculus. SIAM Journal of Computing, 5(3):488–521.
-models of the
lambda-calculus. SIAM Journal of Computing, 5(3):488–521.