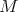is a hereditary permutation if the Böhm tree 
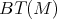has the following properties:
Submitted by Mariangiola Dezani-Ciancaglini
Date: 2006
Statement. Type theoretic characterisation of hereditary permutations
According to [Bergstra and Klop, 1980, Barendregt, 1984] (Definition 21.2.9)
a closed lambda-term 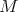is a hereditary permutation if the Böhm tree
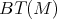has the following properties:
does not occur in 
;
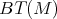The problem is to find a type assignment system in which all and only the hereditary
permutations get types of a fixed shape.
Many other sets of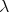 
-terms have been characterised in this way, see for
example [Kurata, 2002, Dezani-Ciancaglini et al., 2005] and the references there.
Solution: Makoto Tatsuta proved [Tatsuta, 2008] that the set of all hereditary permutations is not recursively enumerable, and therefore cannot be characterized by typability in a finitary type-assignment system. On the other hand, there is a system such that a term can be assigned a certain countably infinite family of types in that system if and only if it is a hereditary permutation.
[Barendregt, 1984] Barendregt, H. (1984). The Lambda Calculus. Its Syntax and Semantics. North-Holland, second edition.
[Bergstra and Klop, 1980] Bergstra, J. A. and Klop, J. W. (1980). Invertible terms in the lambda calculus. Theoretical Computer Science, 11:19–37.
[Dezani-Ciancaglini et al., 2005] Dezani-Ciancaglini, M., Honsell, F.,
and Motohama, Y. (2005). Compositional characterization of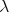 
-terms
using intersection types. Theoretical Computer Science, 340(3):459–495.
[Kurata, 2002] Kurata, T. (2002). Intersection and singleton type assignment characterizing finite Böhm-trees. Information and Computation, 178(1):1–11.
[Tatsuta, 2008] Tatsuta, M. (2008). Types for hereditary permutators. In Proceedings of the Twenty-Third Annual IEEE Symposium on Logic in Computer Science, LICS 2008, 24-27 June 2008, Pittsburgh, PA, USA. http://nii.ac.jp/TechReports/07-010E.html .