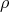is a retract of
a type 
(write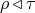 
) iff there exists a type environment 
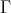and terms
Submitted by Paweł Urzyczyn
Date: 2007
Statement. Is higher-order matching decidable with many atoms?
It has recently been proved [Stirling, 2009] that the higher-order matching problem is decidable. However, the proof method only applies to the “classical” case of the problem: when all types are built from a single atom. Therefore, the problem remains open for the generalized case of types built from an arbitrary number of type variables.
A special case of the higher-order matching problem is the retraction problem,
first mentioned in [de’Liguoro et al., 1992]. We say that a type 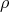is a retract of
a type (write 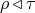) iff there exists a type environment 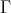and terms
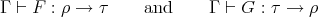
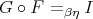. The problem to decide if 
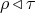holds for given 
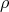and
is decidable for a single atom [Padovani, 2001] but for many atoms it
remains an open question. For a discussion see [Regnier and Urzyczyn,
2001].
Even less is known about polymorphic retractions. For instance, it is
conjectured that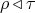 
and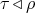 
implies that 
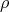and 
are isomorphic. A
confirmation of this conjecture yields a negative answer to Problem 17,
see [Regnier and Urzyczyn, 2001].
[de’Liguoro et al., 1992] de’Liguoro, U., Piperno, A., and Statman, R. (1992). Retracts in simply typed lambda-beta-eta-calculus. In Logic in Computer Science, pages 461–469. IEEE Computer Society Press.
[Padovani, 2001] Padovani, V. (2001). Retracts in simple types. In Abramsky, S., editor, Typed Lambda Calculi and Applications, volume 2044 of Lecture Notes in Computer Science, pages 376–384. Springer-Verlag.
[Regnier and Urzyczyn, 2001] Regnier, L. and Urzyczyn, P. (2001). Retractions of types with many atoms. Technical Report 29, IML Marseille. http://arxiv.org/abs/cs/0212005.
[Stirling, 2009] Stirling, C. (2009). Decidability of higher-order matching. Logical Methods in Computer Science, 5(3).