Date: 2002
Statement. Does easiness imply simple easiness?
Problem Origin. The problem was posed by Fabio Alessi and Mariangiola Dezani-Ciancaglini .
Submitted by Mariangiola Dezani-Ciancaglini
Date: 2002
Statement. Does easiness imply simple easiness?
Problem Origin. The problem was posed by Fabio Alessi and Mariangiola
Dezani-Ciancaglini .
According to [Jacopini, 1975] a closed term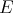 
is easy if, for any other closed
term 
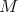, the theory 
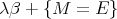is consistent.
[Alessi and Lusin, 2002] introduce the notion of simple easiness: roughly a
term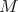 
is simple easy if given an arbitrary intersection type 
one can find a
suitable pre-order on types which allows to derive 
for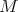 
. In the same paper
the authors show that for each simple easy term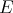 
and for each arbitrary closed
term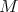 
it is possible to build a 
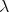-model in which the interpretations of 
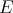and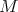 
coincide.
Clearly each simple easy term is easy, but the vice versa is open.
Remark: The content of [Alessi et al., 2004] are some applications of simple easiness.
Solution: Alberto Carraro and Antonino Salibra announced a solution in February 2010, the solution is published in [Carraro and Salibra, 2012].
[Alessi et al., 2004] Alessi, F., Dezani-Ciancaglini, M., and Lusin, S. (2004). Intersection types and domain operators. Theoretical Computer Science, 316(1–3):25–47.
[Alessi and Lusin, 2002] Alessi, F. and Lusin, S. (2002). Simple easy terms. In van Bakel, S., editor, Intersection Types and Related Systems, volume 70 of Electronic Notes in Computer Science. Elsevier.
[Carraro and Salibra, 2012] Carraro, A. and Salibra, A. (2012). Easy lambda-terms are not always simple. RAIRO - Theoretical Informatics and Applications, 46:291–314.
[Jacopini, 1975] Jacopini, G. (1975). A condition for identifying two
elements of whatever model of combinatory logic. In Böhm, C., editor,
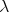-Calculus and Computer Science Theory, volume 37 of Lecture Notes
in Computer Science, pages 213–219. Springer-Verlag.