Date: Known since 1958!
Statement. Is there a direct proof of the confluence of
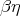-strong reduction?
Problem Origin. First posed by Haskell Curry and Roger Hindley.
Submitted by Roger Hindley
Date: Known since 1958!
Statement. Is there a direct proof of the confluence of 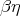-strong reduction?
Problem Origin. First posed by Haskell Curry and Roger Hindley.
The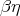 
-strong reduction is the combinatory analogue of 
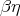-reduction in
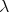-calculus. It is confluent. Its only known confluence-proof is very easy, [Curry
and Feys, 1958, 
6F, p. 221 Theorem 3], but it depends on the having already
proved the confluence of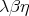 
-reduction. Thus the theory of combinators is
not self-contained at present. Is there a confluence proof independent of
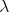-calculus?
Warning: Like a bog, the theory of strong reduction is messier than it looks at
first; see [Curry and Feys, 1958, 
6F], [Curry et al., 1972, 
11E], [Hindley and
Seldin, 1986, Ch. 9], and sources cited therein.
Solution: Two independent confluence proofs have been proposed in June 2008: one by René David [David, 2009], the other by Pierluigi Minari [Minari, 2009].
[Curry and Feys, 1958] Curry, H. B. and Feys, R. (1958). Combinatory Logic, Volume I. North-Holland, Amsterdam. (3rd edition 1974).
[Curry et al., 1972] Curry, H. B., Hindley, J. R., and Seldin, J. P. (1972). Combinatory Logic, Volume II. North-Holland, Amsterdam.
[David, 2009] David, R. (2009). A direct proof of the confluence of combinatory strong reduction. Theoretical Computer Science, 410(42):4204–4215.
[Hindley and Seldin, 1986] Hindley, J. R. and Seldin, J. P. (1986).
Introduction to Combinators and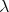 
-calculus. Cambridge University
Press.
[Minari, 2009] Minari, P. (2009). A solution to Curry and Hindley’s problem on combinatory strong reduction. Archive for Mathematical Logic, 43(2):159–184.