Problem # 2 [SOLVED]

Submitted by Roger Hindley
Date: Known since 1973!
Statement. Is ticket entailment decidable? $\text{[math]}$
Problem Origin. The problem was ﬁrst posed by Robert Meyer.

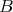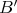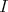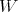The question is whether there is a decision-algorithm for the implicational fragment T $→$ of the propositional logic called ticket entailment. Equivalently, is there one for the simple type-theory of the restricted combinatory logic based on $B$ , $′ B$ , $I$ , $W$ ? The logic T $→$ has just one deduction-rule (( $→$ E) or modus ponens), and four axiom-schemes:

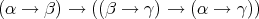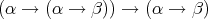Alternatively, let CL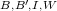 $′ B,B ,I,W$ be the system of combinatory logic whose terms are built by application from four basic combinators with reduction rules:

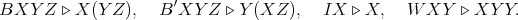
(Abstraction in CL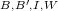 $B,B ′,I,W$ is much weaker than in full combinatory logic; see [Trigg et al., 1994, $§$ 3] for a characterization by P. Trigg.) Let types be built by the operation $(σ → τ)$ from type-variables 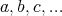$a,b,c,...$ , and let types be assigned to terms as usual, starting from these four axiom-schemes:

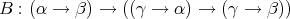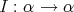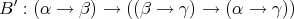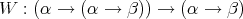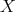Is there an algorithm that, when applied to any type $τ$ , will decide whether there exists a term $X$ in this system such that $X : τ$ is provable?

System T $→$ ﬁrst appeared in print in [Anderson, 1960], although it dates back at least to work of Belnap in 1957. It was motivated and described in detail in [Anderson and Belnap, 1975, Chapter 1 $§§$ 6 and 8.3.2 (pp. 41–50 and 76)]. Its decidability question was ﬁrst raised on p. 69 of that book. Proofs of the decidability and undecidability of several related systems were given in [Anderson et al., 1992, $§ §$ 60–67 (pp. 267–391)]; for example in $§$ 65.2 the logic T of ticket entailment was shown to be undecidable, but the method did not apply to its implicational fragment T $→$ . A decidability result for a restricted class of formulas can be found in [Broda et al., 2004].

Warnings: (1) In the 30 years since 1975 the T $→$ problem and its combinatory equivalent have been tried by several very able workers without success. For example some relevant results are in [Bimbó, 2005] and [Bimbó, 2006].

(2) In papers on entailment, omitted parentheses are usually restored by “association to the left”, not “to the right” as in types in type theory!

Solution: Two independent conﬂuence proofs have been proposed in 2010. The solution by Katalin Bimbó and J. Michael Dunn is published in [Bimbó and Dunn, 2013]. The solution by Vincent Padovani is published in [Padovani, 2013].

References for # 2

[Anderson, 1960] Anderson, A. R. (1960). Entailment shorn of modality. Journal of Symbolic Logic, 25:388. (Abstract).

[Anderson and Belnap, 1975] Anderson, A. R. and Belnap, N. D. (1975). Entailment. The Logic of Relevance and Necessity, Volume 1. Princeton University Press, U.S.A.

[Anderson et al., 1992] Anderson, A. R., Belnap, N. D., and Dunn, J. M. (1992). Entailment. The Logic of Relevance and Necessity, Volume 2. Princeton University Press, U.S.A.

[Bimbó, 2005] Bimbó, K. (2005). Types of I-free hereditary right maximal terms. Journal of Philosophical Logic, 34:607–620.

[Bimbó, 2006] Bimbó, K. (2006). Relevance logics. In Jacquette, D., editor, Philosophy of Logic, volume 5 of Handbook of the Philosophy of Science, pages 723–789. North-Holland/ Elsevier, Amsterdam.

[Bimbó and Dunn, 2013] Bimbó, K. and Dunn, J. M. (2013). On the decidability of implicational ticket entailment. Journal of Symbolic Logic, 78(1):214–236.

[Broda et al., 2004] Broda, S., Damas, L., Finger, M., and e Silva, P. S. (2004). The decidability of a fragment of BB’IW-logic. Theoretical Computer Science, 318(3):373–408.

[Padovani, 2013] Padovani, V. (2013). Ticket entailment is decidable. Mathematical Structures in Computer Science, 23(3):568–607.

[Trigg et al., 1994] Trigg, P., Hindley, J. R., and Bunder, M. W. (1994). Combinatory abstraction using B, B’ and friends. Theoretical Computer Science, 135:405–422.