Date: 1981
Statement. Does the range property hold for the theory
? 
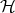Problem Origin. The problem was first posed by Henk Barendregt .
Submitted by Richard Statman
Date: 1981
Statement. Does the range property hold for the theory ?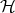
Problem Origin. The problem was first posed by Henk Barendregt .
Consider the least lambda theory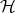 
which equates all unsolvable terms. Take
any combinator 
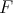. Prove that either 
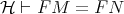, for all closed
, 
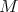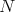, or there are infinitely many closed 
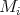, such that no two of
terms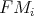 
are equated under 
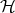. This problem, known as the range
problem for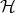 
, is stated as Conjecture 20.2.8 in [Barendregt, 1984].
Comments by Richard Statman: Different researchers have different takes on this problem. Mine are the following.
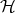is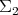 
-complete but there
is no good notion of 
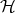-computability that allows the “computation”
of those number theoretic function recursive in jump of 0. If one knew
such a notion of computability then one could copy the usual recursion
theoretic proof of the range property for beta-eta.
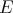such that 
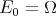and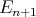 
is the
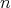-th solvable term. Then one can construct Plotkin terms 
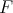and
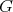such that if 
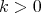then
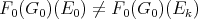
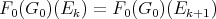
and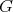 
can be constructed to
be solvable then we would have a term with a range of size 
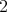for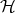 
.Solution: A negative solution has been presented by A. Polonsky in 2010 and published in [Polonsky, 2012], who constructs a term F with a two-element range. In contrast, Intrigila and Statman [Intrigila and Statman, 2011] showed that the range property for Combinatory Logic is true.
[Barendregt, 1984] Barendregt, H. (1984). The Lambda Calculus. Its Syntax and Semantics. North-Holland, second edition.
[Intrigila and Statman, 2011] Intrigila, B. and Statman, R. (2011). Solution to the range problem for combinatory logic. Fundamenta Informaticae, 111(2):203–222.
[Polonsky, 2012] Polonsky, A. (2012). The range property fails for H. Journal of Logic and Computation, 77(4):1195–1210.