Date: 1985
Statement. A fixed point combinator from
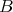and 
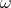alone? 
Problem Origin. The problem was first posed by Raymond Smullyan.
Submitted by Richard Statman
Date: 1985
Statement. A fixed point combinator from 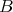and 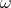alone?
Problem Origin. The problem was first posed by Raymond Smullyan.
The combinator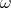 
satisfies the reduction rule 
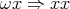and the combinator 
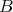is
as usual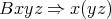 
. Is there an applicative combination of 
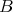and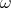 
which is a fixed point combinator? The problem was originally proposed
in [Smullyan, 1985].
Comments by Richard Statman: Note that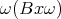 
is always a
fixed point of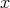 
but it appears that 
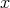cannot be abstracted to give a
fixed point combinator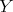 
such that 
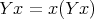. If it is required that
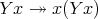as with Turing’s fixed point combinator then it can be
shown [Statman, 1993, McCune and Wos, 1991] that no 
,
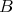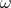combination
works.
[McCune and Wos, 1991] McCune, W. and Wos, L. (1991). The absence and the presence of fixed point combinators. Theoretical Computer Science, 87:221–228.
[Smullyan, 1985] Smullyan, R. (1985). To Mock a Mockingbird. Knopf.
[Statman, 1993] Statman, R. (1993). Some examples of non-existent combinators. Theoretical Computer Science, 121:441–448.