Date: 1993
Statement. Are there terms untypable in
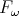 but typable with help of positive
recursive types?
but typable with help of positive
recursive types? Submitted by Paweł Urzyczyn
Date: 1993
Statement. Are there terms untypable in 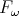 but typable with help of positive
recursive types?
but typable with help of positive
recursive types?
Consider an extension of simply typed lambda-calculus obtained by adding the
construct 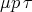 for types
for types  containing only positive occurrences of
containing only positive occurrences of 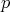 , together
with the rules:
, together
with the rules:
![Γ-⊢-M--: τ[p:=μp-τ-] ---Γ-⊢-M--: μp-τ---
Γ ⊢ M : μp τ Γ ⊢ M : τ[p:= μpτ ]](opltlca106x.png)
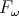 ? Note
that 22K can be typed in
? Note
that 22K can be typed in 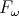 [Urzyczyn, 1997]. Note also that
[Urzyczyn, 1997]. Note also that 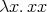 ,
easily typable in system F, is clearly untypable with positive recursive
types.
,
easily typable in system F, is clearly untypable with positive recursive
types.
[Urzyczyn, 1996] Urzyczyn, P. (1996). Positive recursive type assignment. Fundamenta Informaticae, 28(1-2):197–209.
[Urzyczyn, 1997] Urzyczyn, P. (1997). Type reconstruction in 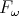 .
Mathematical Structures in Computer Science, 7(4):329–358.
.
Mathematical Structures in Computer Science, 7(4):329–358.