[Next] [Previous] [Up]
Problem # 22
Submitted by Furio Honsell
Date: April 20 2007
Statement. Is there a continuously complete CPO model of the 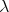 -calculus
whose theory is precisely
-calculus
whose theory is precisely 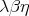 or
or 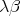 ?
? 
Problem Origin. I asked myself this question in 1983. In 1984, on different
occasions I asked it to Dana Scott and Gordon Plotkin. Both told me that they
had already thought about it.
[PRINT this PROBLEM]
A CPO model is continuously complete if all Scott-continuous self-maps are
represented by a point in the model. Continuously complete models are sometimes
called retract models or reflexive models.
The theory of a model is the set of all equations between closed 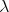 -terms
which hold in the model. The problem can be phrased equivalently as:
-terms
which hold in the model. The problem can be phrased equivalently as:
- Is
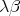 (or
(or 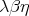 ) the only equations which hold in all (extensional)
continuously complete CPO models of
) the only equations which hold in all (extensional)
continuously complete CPO models of 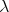 -calculus? I.e. Are retract
models complete for
-calculus? I.e. Are retract
models complete for 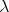 -calclulus?
-calclulus?
- Is there a filter model whose theory is precisely
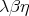 or
or 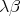 ?
?
There are many related results, e.g.:
There exists a 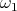 -continuously complete
-continuously complete 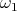 -CPO model whose theory is
precisely
-CPO model whose theory is
precisely 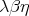 [Di Gianantonio et al., 1995].
[Di Gianantonio et al., 1995].
There exist theories which do not have continuously complete CPO-models
[Honsell and Ronchi Della Rocca, 1992].
References for # 22
[Di Gianantonio et al., 1995] Di Gianantonio, P., Honsell, F., and
Plotkin, G. (1995). Uncountable limits and the lambda calculus. Nordic
Journal of Computing, 2(2):126–145.
[Honsell and Ronchi Della Rocca, 1992] Honsell, F. and Ronchi Della
Rocca, S. (1992). An approximation theorem for topological lambda
models and the topological incompleteness of lambda calculus. Journal of
Computer and System Sciences, 45(1):49–75.
[Next] [Previous] [Up]
Last modified: July 21, 2014
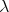 -calculus
whose theory is precisely
-calculus
whose theory is precisely 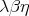 or
or 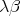 ?
? 
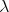 -terms
which hold in the model. The problem can be phrased equivalently as:
-terms
which hold in the model. The problem can be phrased equivalently as:
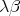 (or
(or 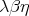 ) the only equations which hold in all (extensional)
continuously complete CPO models of
) the only equations which hold in all (extensional)
continuously complete CPO models of 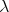 -calculus? I.e. Are retract
models complete for
-calculus? I.e. Are retract
models complete for 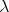 -calclulus?
-calclulus?
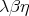 or
or 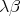 ?
?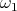 -continuously complete
-continuously complete 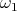 -CPO model whose theory is
precisely
-CPO model whose theory is
precisely