Date: 1992
Statement. Does Expansion Postponement hold for every PTS?

Problem Origin. This property was first conjectured by Pollack [Pollack, 1992] .
Submitted by Robin Adams
Date: 1992
Statement. Does Expansion Postponement hold for every PTS? 
Problem Origin. This property was first conjectured by Pollack [Pollack, 1992]
.
We can replace the usual conversion rule in a Pure Type System (PTS):
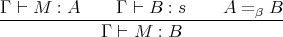
with the following two rules:
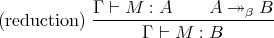
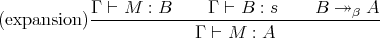
Expansion Postponement (EP) is the conjecture that every derivable judgement in a PTS has a derivation in which the expansion rule is used at most once, as the final step in the derivation.
This was proposed by Pollack in 1992 [Pollack, 1992], where he showed that it is a necessary condition for the type-checking algorithm given there to be complete. Gutiérrez and Ruiz [Gutiérrez and Ruiz, 2003] proved that it is a necessary condition for cut elimination in a sequent calculus formulation of PTSs.
It was shown by Erik Poll [Poll, 1998] to hold for every weakly normalising PTS, and by Barthe [Barthe, 1998] to hold for injective PTSs.
[Barthe, 1998] Barthe, G. (1998). Type-checking injective pure type systems. Journal of Functional Programming, 9:675–698.
[Gutiérrez and Ruiz, 2003] Gutiérrez, F. and Ruiz, B. (2003). Cut elimination in a class of sequent calculi for pure type systems. Electronic Notes in Computer Science, 84:105–116.
[Poll, 1998] Poll, E. (1998). Theoretical pearl: Expansion postponement for normalising pure type systems. Journal of Functional Programming, 8:89–96.
[Pollack, 1992] Pollack, R. (1992). Typechecking in Pure Type Systems. In Informal Proceedings of the 1992 Workshop on Types for Proofs and Programs, Bastad, Sweden, pages 271–288.